近日清华大学交叉信息研究院徐勇研究组在拓扑凝聚态物理领域取得重要进展，首次在理论上预言三维二阶拓扑绝缘体可以在完全随机点阵即无定形体系中存在，并发现结构无序可以诱发拓扑平庸相到二阶拓扑绝缘体的量子相变。研究人员还提出在实空间中计算三维二阶拓扑绝缘体拓扑不变量的方法（包括有时间反演对称性的体系）。该成果的研究论文《结构无序诱导的三维二阶拓扑绝缘体》（Structural-Disorder-Induced Second-Order Topological Insulators in Three Dimensions）于近日刊发于国际物理学期刊《物理评论快报》（Physical Review Letters）。

     最近，高阶拓扑绝缘体在物理学的各个领域获得广泛关注。考虑一个维系统，这类新型拓扑绝缘体具有n-m( 1<m ≤ n)维无能隙边界态。由于无定形材料在自然界中广泛存在，一个很自然的问题是无定形系统中是否可以存在高阶拓扑绝缘体。之前的研究表明三维二阶拓扑绝缘体需要晶格对称性保护。考虑到无定形系统没有晶格对称性，这似乎意味着三维系统中不能存在二阶拓扑绝缘体。

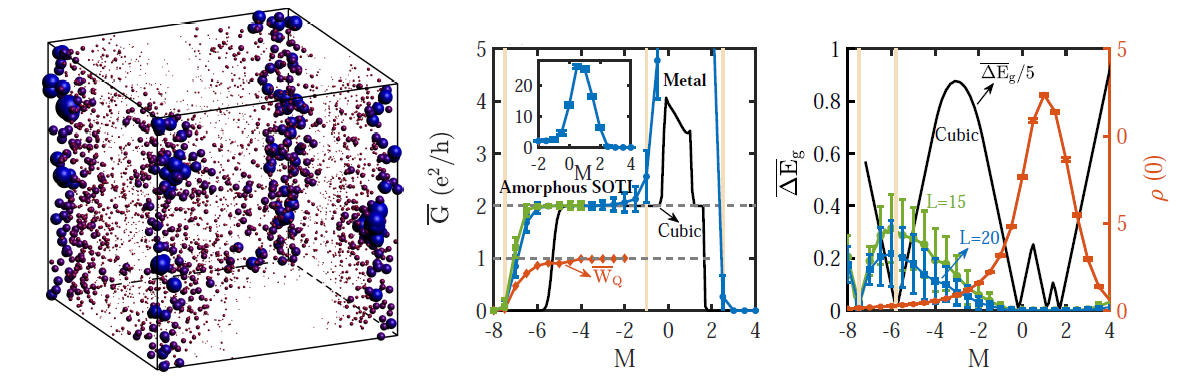
所研究体系链边界态示意图和计算结果

               在此项工作中，研究人员发现三维无定形体系中可以存在二阶拓扑绝缘体，并且结构无序可以诱导出二阶拓扑绝缘体。这意味着在某些条件下无定形系统相比于晶格系统更容易出现二阶拓扑绝缘体。具体而言，研究人员计算了三维随机点阵的二端电导，发现在一个参数区间内，平均电导量子化到2e² / h，表明该三维体系的棱上存在无能隙的边界态。另外，研究人员发现这种绝缘体由四极矩的绕数保护，因此不需要晶格对称性。研究人员还发现在一个参数范围内，在平庸晶格体系中加入格点位置的随机偏移会引起二端电导从0到2e² / h 的跃变。另外，随着结构无序的增加，局域态密度表明链边界态的出现。以上证据表明结构无序可以诱导出二阶拓扑绝缘体。最后，研究人员考虑时间反演对称性体系，提出两种新的拓扑不变量在实空间刻画二阶拓扑绝缘体的性质。具体计算也表明二阶拓扑绝缘体也可以存在于三维具有时间反演对称性的无定形系统中。此项工作表明高阶拓扑相可能在无定形体系中广泛存在，对于进一步理解无序、对称性和拓扑的关系具有重要意义。

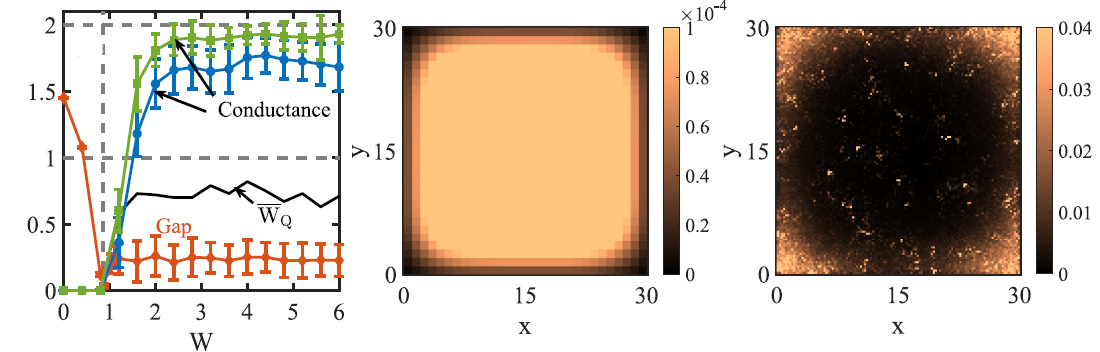
结构无序诱导的三维二阶拓扑绝缘体

         该论文共同第一作者为清华大学交叉信息研究院在读博士生王炅昊（2020级）和杨炎彬（2015级），通讯作者为徐勇助理教授，其他作者包括交叉信息研究院博士后戴凝。该项目得到国家自然科学基金、清华大学引进人才启动经费和上海期智研究院的资助与支持。