近日,根据计算机科学领域顶级国际会议第54届ACM计算理论年会(STOC 2022 54th Annual Symposium on the Theory of Computing)官网公布,交叉信息院师生及校友共有7篇论文被接收,其中计科班91班范致远、计科92班李嘉图与杨天祺,三位同学共同完成的论文《The Exact Complexity of Pseudorandom Functions and the Black-Box Natural Proof Barrier for Bootstrapping Results in Computational Complexity》被大会接收,并获评最佳学生论文。
最佳学生论文
The Exact Complexity of Pseudorandom Functions and the Black-Box Natural Proof Barrier for Bootstrapping Results in Computational Complexity
伪随机函数(pseudorandom functions)是无法与随机函数区分开的函数族。它作为密码学许多构造的起点,是密码学的基础。因此构造高效的伪随机函数在理论及应用中有多种意义。论文研究了伪随机函数的电路复杂性,在多个重要的电路复杂性类中对伪随机函数给出了紧的上界与下界。例如证明了在一般电路中,若多项式大小的电路可计算的伪随机函数存在,则存在一个仅需大约2n个门的电路族即可计算的伪随机函数。同时,该研究无条件地证明了计算任何伪随机函数至少需要2n-2个门。
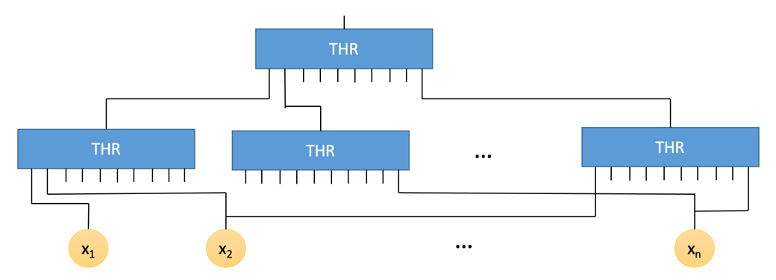
两层线性阈门电路
这些上下界结果为电路复杂性理论提供了新的理解,也解释了为何一些广为相信的猜想难以被证明。特别地,针对目前电路复杂性理论中存在许多被称为"bootstrapping phenomena"的现象,该研究指出,要想从这些现象推出P vs NP等重要开放问题的答案,还需要一些全新的证明思路。
文章作者:范致远(计科91)、李嘉图(计科92)、杨天祺(计科92)
文章链接: https://eccc.weizmann.ac.il/report/2021/125/
被接收论文
(Fractional) Online Stochastic Matching via Fine-Grained Offline Statistic
在线随机匹配问题是为了研究互联网显示广告,由Feldman, Mehta, Mirrokni, and Muthukrishnan (FOCS 2009)提出的。在独立同分布的在线随机二分图匹配问题中,一侧节点是固定的离线节点,另一侧是在线到达的节点。该研究把每个在线节点的连边情况叫做它的类别。在开始之前,算法知道所有的离线节点,以及每个在线到达的节点类别的分布(所有在线节点满足独立同分布)。对于每个在线的到达的节点,算法在它到达时刻会知道它的类别,并且必须不可反悔的决定它如何匹配。在离线节点带权的情况中,想要让被匹配的离线点期望权值和最大。在研究中,把这个模型推广到了离线节点带权、并且在线节点不同分布的情况。文章对同分布和不同分布的情况分别设计了竞争比为 0.718 和 0.731 的分数匹配算法,通过用 Gao et al. (FOCS 2021) 提出的在线相关选择,该研究可以把它们取整成为竞争比分别为 0.666 和 0.704 的整数匹配算法。

在线随机匹配的一个下界
文章作者: 武弘勋(计科81)、其他合作者
文章链接:https://arxiv.org/abs/2204.06851
3.1n − o(n) Circuit Lower Bounds for Explicit Functions
电路复杂性(circuit complexity)是复杂性理论中广为关注的问题。其中一个经典结论是大多数语言都需要指数级大小的电路才足以进行判定,但是该结论的证明是非构造性的。给出一个需要很大的电路才能判定的具体语言是有几十年历史的开放问题。在此之前,最好的结果是Find, Golovnev, Hirsch, and Kulikov于2016年给出的:存在一个多项式可计算的语言不能被(3+1/86)n-o(n)大小的电路计算。该研究改进了他们的方法,证明了同一个语言不能被3.1n-o(n)大小的电路计算。
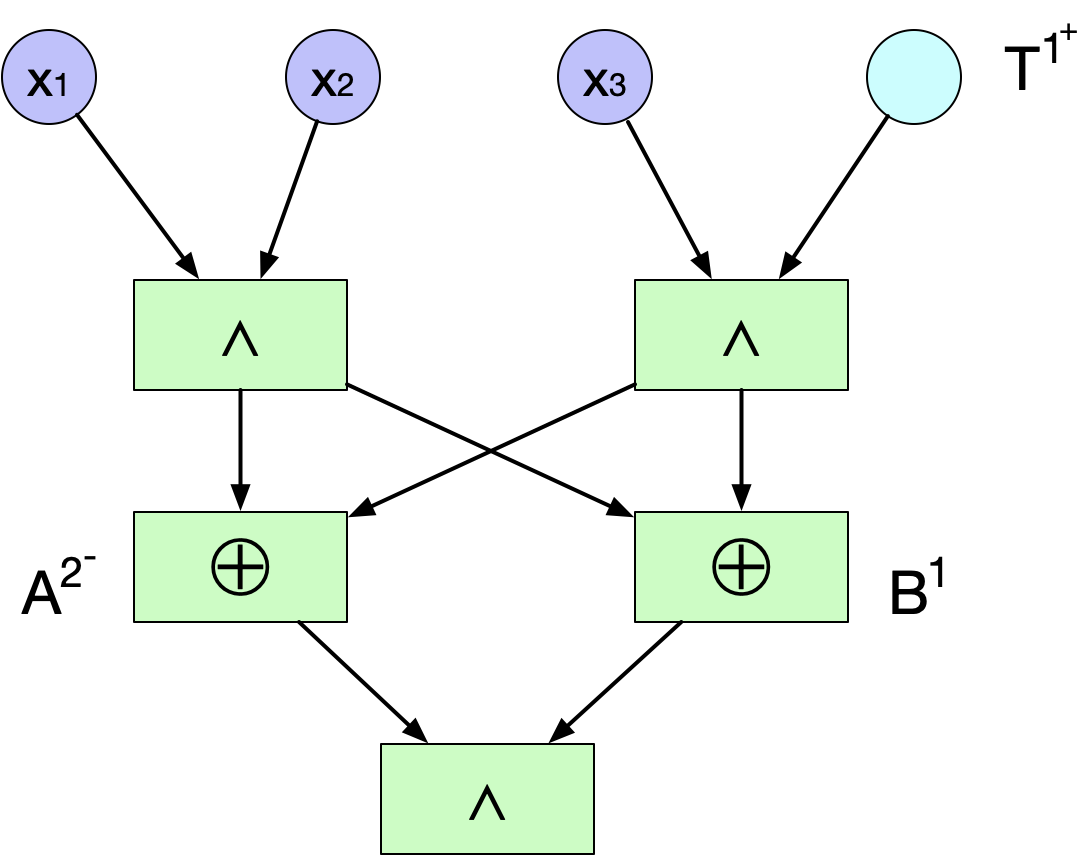
一般电路的结构
文章作者:李嘉图(计科92)、杨天祺(计科92)
文章链接:https://eccc.weizmann.ac.il/report/2021/023/
Optimal Vertex Connectivity Oracles
该论文研究了k-点连通性数据结构。在无向图中如果两点之间最多有k条不相交的路径,就称这两点间的点连通度是k。在k-点连通性数据结构中,我们可以快速查询任意两点间的点连通度如果点连通度不大于k,否则回答³k。本论文改进了之前最好的结构[Iszak & Nutov 2012]中的查询时间和建造时间,使得查询时间从O(k log n)改进到O(log n),做到与k无关,而建造时间改进到接近最大流问题所需时间。本论文还证明了k-点连通性数据结构的空间下界为Ω(nk/log n) ,说明了Iszak和Nutov的结构和本论文提出的结构中所需空间接近最优。

k-点连通性示意图
文章作者:尹龙晖(2021届姚班校友/2021级交叉信息院研究生)、其他合作者
文章链接:https://arxiv.org/abs/2201.00408
Maintaining Exact Distances under Multiple Edge Failures
该论文研究多边失效时精确最短路数据结构,即对一个无向有权图,我们希望建造一个数据结构,使得当最多d条边失效时仍能快速查询任意两点间的距离。此前的结果包括最多两条边或两个点失效时精确最短路结构[Duan & Pettie 2009]、无向图中d条边失效时[Chechik et al. 2017]和d个点失效时[Duan, Gu, Ren 2021]近似最短路结构。论文给出第一个高效的d条边失效时精确最短路结构。对任意常数d,空间复杂度为O(dn^4),查询时间为d^{O(d)}。
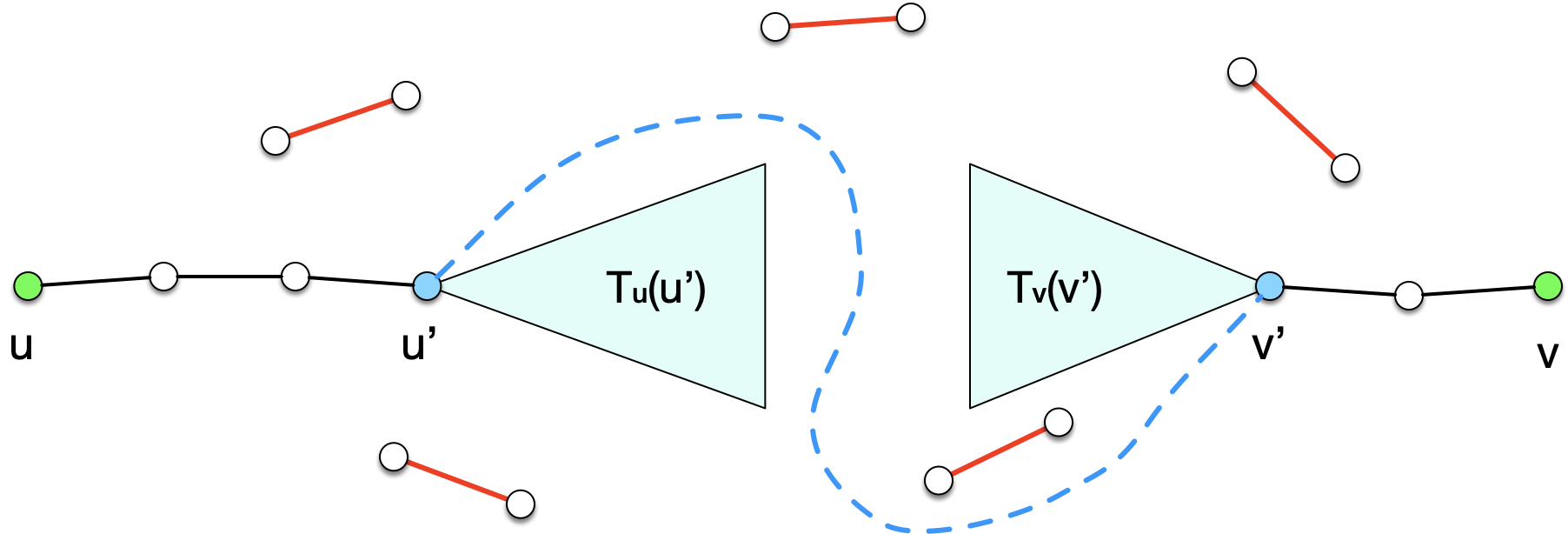
多边失效时最短路数据结构设计示意图
文章作者: 段然(交叉信息院副教授)、任瀚林(2021届姚班校友)
文章链接:https://arxiv.org/abs/2111.03360
Faster Min-Plus Product for Monotone Instances
该论文给出了更快的单调矩阵的(min,+)-乘法算法。(min,+)-矩阵乘法是算法领域的经典难题,因其与每两点间最短路问题等价。对于n×n矩阵,目前仍然没有真正的快于立方时间的算法。当A为任意矩阵,B的每行(或每列)都是单调非递减,并且B中的元素大小是O(n)时,我们给出了时间复杂度为O(n^{2.686})的新算法,改进了之前O(n^{2.875})的算法[Gu et al. 2021],同时也将一些能归约到这个问题的其他问题的时间复杂度改进到了O(n^{2.686}),包括有限差矩阵(即相邻元素的差为常数)的(min,+)-矩阵乘法。[Bringmann et al. 2016]证明了很多问题,像上下文无关文法的带权分析和编辑距离、RNA-折叠、栈生成等,都可以归约到有限差矩阵的(min,+)-矩阵乘法,所以这些问题的复杂度都被改进到了O(n^{2.686})。该研究还改进了单调数组的(min,+)-卷积问题的时间复杂度。
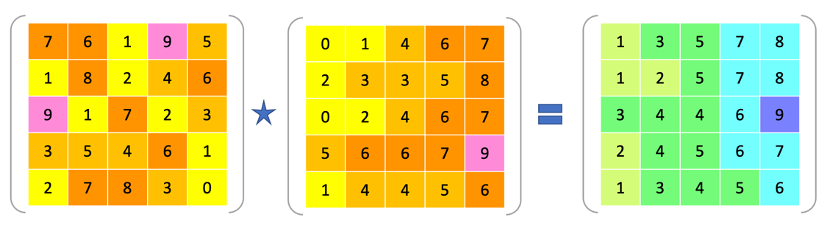
任意矩阵与单调矩阵的距离乘法
文章作者:迟舒乘(2021届姚班校友/2021级交叉信息院研究生)、谢添乐(2021届姚班校友/2021级交叉信息院研究生)、张天翼(2016届姚班校友/2021届交叉信息院研究生校友)、段然(交叉信息院副教授)
文章链接:https://arxiv.org/abs/2204.04500
The Power of Multiple Choices in Online Stochastic Matching
此前,在线随机匹配问题的一系列算法只对每个在线节点考虑两个相邻的离线节点作为潜在匹配目标。这篇文章介绍了两种考虑多个潜在匹配目标的新算法。在无权或带点权的情况下,我们采用在线相关选择技术将近似比提升到了0.716。在带边权且允许离线节点事后选择的情况下,我们通过分析整个匹配的权值随时间变化的函数将近似比提升到了0.706,这是在这个模型下的第一个近似比超过1-1/e的算法。对于一般的带边权的情况,我们证明了近似比存在0.703的上界,将它与以上三种模型区分开来。

在线匹配的前一半随机采样算法示意图
文章作者: 闫书弈(计科81)、黄志毅(2008届姚班校友)、 束欣凯(2019届姚班校友)
文章链接:https://arxiv.org/abs/2203.02883
关于STOC
ACM计算理论年会(STOC)是理论计算机科学领域最顶级的国际会议,在整个计算机科学领域享有崇高的声望,并被公认属于难度最高的会议之一。STOC2022将于意大利罗马召开,本次会议共接收论文投稿457篇,录用135篇,接收率约为29%。