交叉信息院量子信息中心金奇奂副教授带领的离子量子计算研究小组新近在囚禁离子系统中成功实现声子算术操作。研究论文《囚禁离子系统中的声子算术实验》于4月21日发表在《自然·通讯》杂志上。论文通讯作者为金奇奂副教授和英国伦敦帝国理工大学的金明湜(Myungshik Kim)教授，共同第一作者为交叉信息院的在读博士生严马可和张君华。

量子粒子中的确定性算术操作（即加法和减法）虽然看似简单，但由于其量子理论是建立在数学结构之上，并且与传统算术操作完全不同，因此在量子设备中实现起来要复杂、困难。

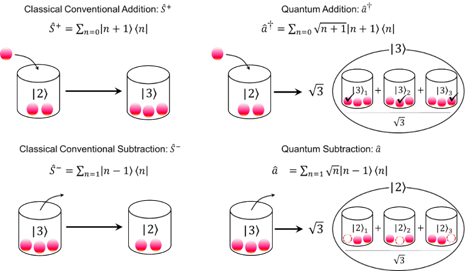
图1：经典算术与量子算术的基本差异。经典算术当中，我们可以确定性地加、减一个粒子，但在量子力学中，加、减一个粒子的概率依赖于已经存在的个数，使其成为概率性操作.

金奇奂实验组使用囚禁离子系统的声子，首次在量子粒子上实现了确定性的加法与减法。实验组采用新开发的绝热量子操控技术将声子耦合到一个辅助的二能级系统，这个系统被称为离散与连续变量混合模式。在具体实验中，实验组在声子数态的叠加态、相干态等不同量子初始态上演绎算术操作，观察得到末态魏格纳函数上的亚泊松统计负值，从而证明了经典态在算术操作之后变成了非经典态。

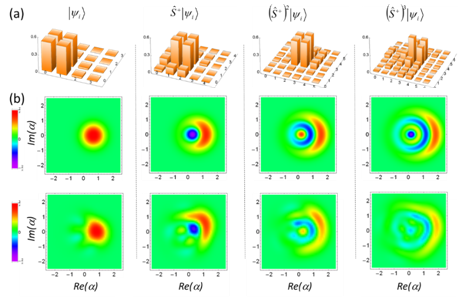
图 2声子加法的实验结果. (a) 对叠加态 做加法. (b) 对相干态 进行加法操作后的函数。上面四张图是理论值，下面四张图是实验数据.

传统算术操作具备多重优点，能够产生确定的非经典态和非高斯态，并且能够提供有效的量子态工程方案。金奇奂实验组的新方案则可以进一步应用到腔量子电动力学、光力学等更多量子光学装备上。该实验项目同时还指出，声子态中的非高斯信息可以通过声子-光子耦合转移到光子态。

本实验由交叉信息院的博士研究生严马可、张君华、吕定顺、路尧和安硕明共同完成，其中严马可为韩国籍留学生。张静宁博士、罗贤铁(Hyunchul Nha)教授、金明湜(Myungshik Kim)教授提供实验的理论支持。此项研究工作得到国家重点基础研究发展计划和国家自然科学基金支持。

论文链接：

http://www.nature.com/ncomms/2016/160421/ncomms11410/full/ncomms11410.html